Показательный (экспоненциальный) закон распределения и распределение Вейбулла

Определение. Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения с параметром X > 0, если ее плотность вероятности имеет вид

Кривая распределения ф(х)и график функции распределения Р(х) случайной величины X приведены на рис. 4.4, а, б.
Теорема. Функция распределения случайной величины X, распределенной по показательному (экспоненциальному) закону, есть

ее математическое ожидание а дисперсия
? При х 0 по формуле (3.23)

т.е. формула (4.22) доказана.
Найдем математическое ожидание случайной величины X, используя при вычислении метод интегрирования по частям:

Для нахождения дисперсии О(Х) вначале найдем



с учетом того, что во втором слагаемом несобственный интеграл есть Теперь
Из доказанной теоремы следует, что для случайной величины, распределенной по показательному закону, математическое ожидание равно среднему квадратическому отклонению, т.е.

Показательный закон распределения играет большую роль в теории массового обслуживания и теории надежности. Так, например, интервал времени Г между двумя соседними событиями в простейшем потоке имеет показательное распределение с параметром X — интенсивностью потока (см. параграф 7.3).
Показательный закон распределения (и только он в классе непрерывных случайных величин) обладает важным свойством, рассматриваемым ниже.
?> Пример 4.7. Доказать, что если промежуток времени Т, распределенный по показательному закону, уже длился некоторое время т, то это никак нс влияет на закон распределения оставшейся части Г, =Т — т промежутка, т.е. закон распределения 7 остается таким же, как и всего промежутка Т.
Решение. Пусть функция распределения промежутка Т определяется по формуле (4.22), т.е. Д?) = 1 — е _5и , а функция распределения оставшейся части Т1 = Т- т при условии, что событие Т > х произошло, есть условная вероятность события Г, т, т.е.
Щ=Рт>Аъ т), В = [Т т) и 7’, = 7’ — т 4 5 (Г>т) = 1-Р(Г ; ‘(т), то выражение (4.25) можно представить в виде

Учитывая формулу (4.22), получим
Доказанное в примере 4.7 свойство «отсутствия последействия» показательного распределения широко используется в марковских случайных процессах (см. гл. 7) [1] .
|> Пример 4.8. Установлено, что время ремонта телевизоров есть случайная величина X, распределенная по показательному закону. Определить вероятность того, что на ремонт телевизора потребуется не менее 20 дней, если среднее время ремонта телевизоров составляет 15 дней. Найти плотность вероятности, функцию распределения и среднее квадратическое отклонение случайной величины X.

Решение. По условию математическое ожидание откуда
параметр = 1/15 и по формулам (4.21) и (4.22) плотность вероятности и функция распределения имеют вид

Искомую вероятность Р(Х > 20) можно было найти по формуле (3.22), интегрируя плотность вероятности, т.е.

но проще это сделать, используя функцию распределения:

Осталось найти среднее квадратическое отклонение а,. = М(Х) = 15 дней. ? Показательное (экспоненциальное) распределение является частным случаем распределения Вейбулла.
Определение. Непрерывная случайная величина X имеет распределение Вейбулла с параметрами а > 0 и X > 0, если ее плотность вероятности имеет вид:

Теорема. Функция распределения случайной величины, распределенной по закону Вейбулла, имеет вид

? При х 0 по формуле (3.23)

?
Распределение Вейбулла имеет широкое применение в теории надежности для описания времени безотказной работы элементов различных устройств, жизни человека (другой биосистемы).
Известно, что интенсивность отказов элементов (коэффициент смертности) Х(1) определяется соотношением

т.е. представляет отношение доли выбывших в возрасте ? элементов к общему числу доживших до этого возраста элементов.

Решение этого дифференциального уравнения (напомним, что ^'(0 = ф(0) показывает, что конкретный вид функции распределения /•’(?) полностью определяется видом функции интенсивности отказов /.(?).
Функция отказов Ц?) (по результатам многочисленных экспериментальных исследований в области надежности) имеет характерный вид кривой, изображенной на рис. 4.5.
На графике Л,(?) четко выделяются три временных периода (см. рис. 4.5): приработка (? ?2). Указанные три периода функции интенсивности отказов получаются, если использовать достаточно гибкое и удобное распределение Вей- булла, при котором при а 1 — возрастает (период старения (износа)). При а = 1 (период нормальной эксплуатации) распределение Вейбулла представляет показательное (экспоненциальное) распределение с постоянной интенсивностью отказа Х<1) = X.
2.Показательный (экспоненциальный закон распределения).
Случайная величина Х распределена по показательному закону распределения с параметром λ, если её плотность вероятности имеет вид:
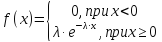
Функция распределения имеет вид:

Математическое ожидание и дисперсия для случайной величины, распределенной по показательному закону, находятся по формулам:
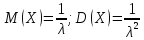
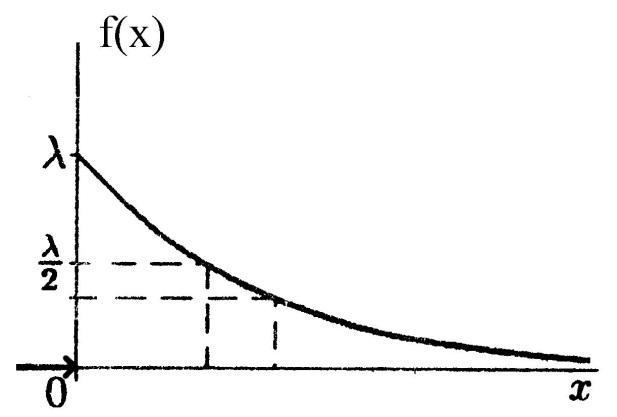

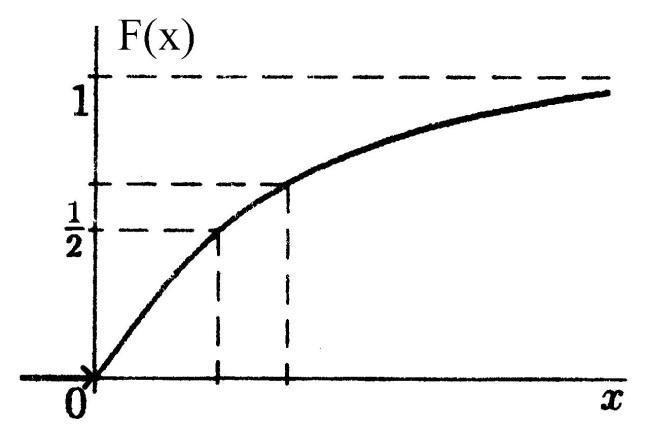
То есть при
Установлено, что время ремонта телевизоров есть случайная величина X, распределенная по показательному закону.
Определить вероятность того, что на ремонт телевизора потребуется не менее 20 дней, если среднее время ремонта телевизоров составляет 15 дней. Найти плотность вероятности, функцию распределения и среднее квадратическое отклонение случайной величины X.
По условию математическое ожидание M(х)=1/λ = 15, откуда параметр λ = 1/15. Тогда плотность вероятности и функция распределения примут вид:
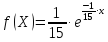

Искомую вероятность P(Х ≥20) можно было найти по формуле, интегрируя плотность вероятности, то есть
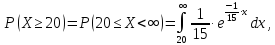
но проще это сделать, используя функцию распределения:
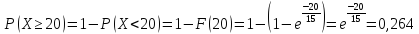
Найдем среднее квадратическое отклонение: σ(X) = М(Х) = 15 дней.
3.Равномерный закон распределения.
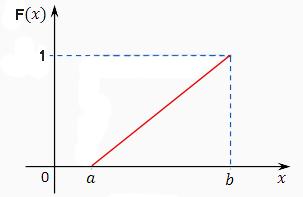
Непрерывная случайная величина Х имеет равномерный закон распределения (закон постоянной плотности) на отрезке [a; b], если на этом отрезке функция плотности вероятности случайной величины постоянна, то есть
f (x) имеет вид:
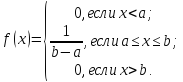

Следовательно, математическое ожидание случайной величины, равномерно распределенной на отрезке (a, b), равняется середине этого отрезка.
Дисперсия имеет вид:
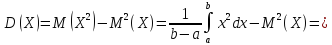
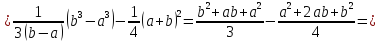
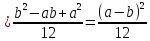
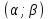
Найдем вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал , принадлежащий целиком отрезку [a, b]:
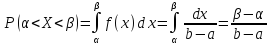
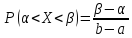
Функция распределения примет вид:

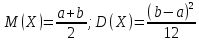

Поезда метрополитена идут регулярно с интервалом 2 мин. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придется не больше полминуты.
Найти математическое ожидание и среднее квадратическое отклонение случайной величины X – времени ожидания поезда.
Случайная величина X – время ожидания поезда на временном (в минутах) отрезке [0;2] имеет равномерный закон распределения f (x)=1/2.
Поэтому вероятность того, что пассажиру придется ждать не более полминуты, равна 1/4 от равной единице площади прямоугольника, т.е.

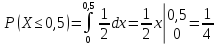
Найдем математическое ожидание, дисперсию и среднее квадратическое отклонение:
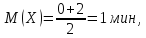

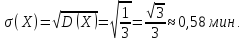
12. Вероятность заданного отклонения. Правило трех сигм.

Теорема. Вероятность модуля отклонения непрерывной случайной величины X от её математического ожидания на величину сколь угодно малого числа ε>0 находится по формуле:
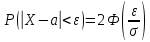
(*)
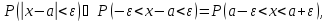
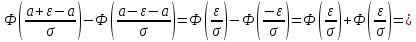
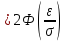
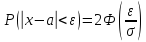
Правило трёх сигм.

Пусть .
Подставим значение ε в формулу (*), получим:
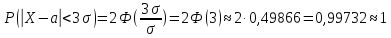
Итак, с вероятностью сколь угодно близкой к единице можно утверждать, что модуль отклонения нормально распределенной случайной величины от её математического ожидания не превосходит утроенного среднего квадратического отклонения.
Центральная предельная теорема.
Центральная предельная теорема представляет собой группу теорем, посвященных установлению условий, при которых возникает нормальный закон распределения. Среди этих теорем важнейшее место принадлежит теореме Ляпунова.
Теорема Ляпунова.

Если случайная величина Х представляет собой сумму большого числа взаимно ‒ независимых случайных величин, то есть, влияние каждой из которых на всю сумму ничтожно мало, то случайная величинаХ имеет распределение, неограниченно приближающееся к нормальному распределению.
Начальные и центральные моменты непрерывной случайной величины, асимметрия и эксцесс. Мода и медиана.
В прикладных задачах, например в математической статистике, при теоретическом изучении эмпирических распределений, отличающихся от нормального распределения, возникает необходимость количественных оценок этих различий. Для этой цели введены специальные безразмерные характеристики.
Определение. Мода непрерывной случайной величины ( Мо (X)) – это её наиболее вероятное значение, для которого вероятность pi или плотность вероятности f(x) достигает максимума.
Определение. Медиана непрерывной случайной величины X (Me(X)) – это такое её значение, для которого выполняется равенство:
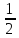
P (X < Me (X)) = P (X >Me (X)) =





















Геометрически вертикальная прямая x = Me (X) делит площадь фигуры под кривой на две равные части.
В точке X = Me (X), функция распределения F (Me (X)) =
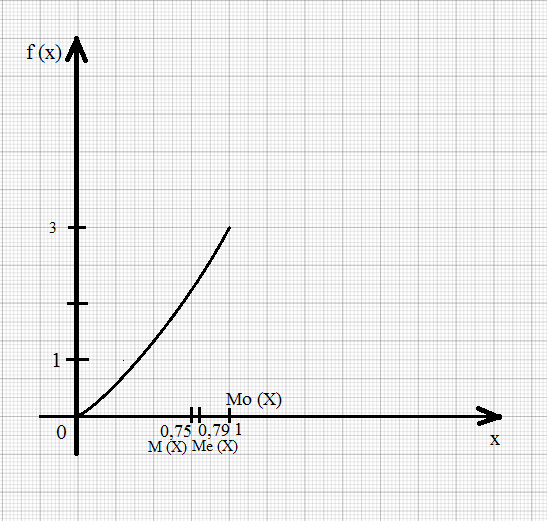
Найти моду Mo, медиану Me и математическое ожидание M случайной величины X с плотностью вероятности f(x) = 3x 2 , при x Î [ 0; 1 ].




Плотность вероятности f (x) максимальна при x = 1, т.е. f (1) = 3, следовательно, Mo (X) = 1 на интервале [ 0; 1 ].
Для нахождения медианы обозначим Me (X) = b.
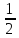
Так как Me (X) удовлетворяет условию P (X < Me (X)) = ,
= = b 3 = .
b 3 = ; b = » 0,79
M (X) = =+=
== = = 0,75
Отметим получившиеся 3 значения Mo (x), Me (X), M (X) на оси Ox:
Определение. Асимметрией теоретического распределения называется отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:
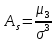
Определение. Эксцессом теоретического распределения называется величина, определяемая равенством:

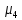
где ‒ центральный момент четвертого порядка.
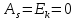
Для нормального распределения . При отклонении от нормального распределения асимметрия положительна, если «длинная» и более пологая часть кривой распределения расположена справа от точки на оси абсцисс, соответствующей моде; если эта часть кривой расположена слева от моды, то асимметрия отрицательна (рис. 1, а, б).
Эксцесс характеризует «крутизну» подъема кривой распределения по сравнению с нормальной кривой: если эксцесс положителен, то кривая имеет более высокую и острую вершину; в случае отрицательного эксцесса сравниваемая кривая имеет более низкую и пологую вершину.
Следует иметь в виду, что при использовании указанных характеристик сравнения опорными являются предположения об одинаковых величинах математического ожидания и дисперсии для нормального и теоретического распределений.
Пример. Пусть дискретная случайная величина Х задана законом распределения:
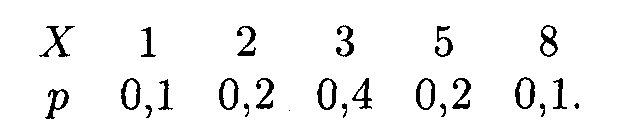
Найти: асимметрию и эксцесс теоретического распределения.
Найдем сначала математическое ожидание случайной величины:
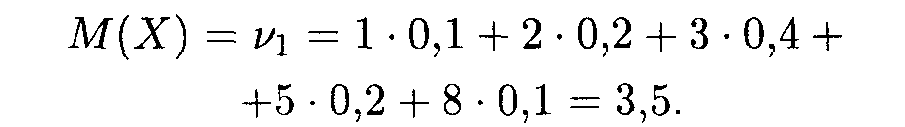
Затем вычисляем начальные и центральные моменты 2, 3 и 4-го порядков и среднее квадратическое отклонение:
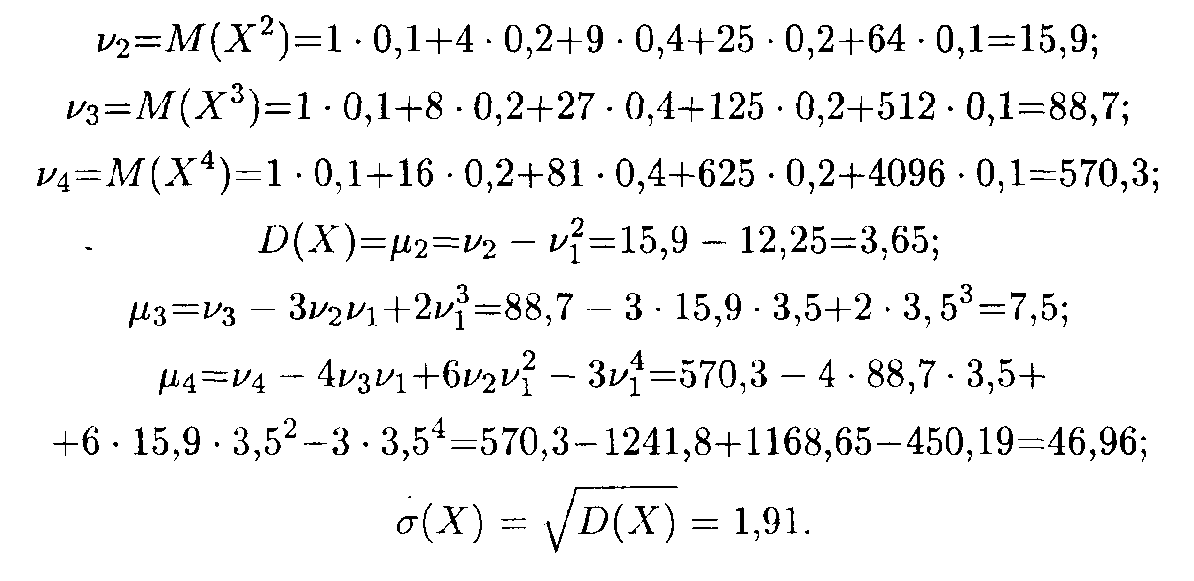
Теперь по формулам находим искомые величины:
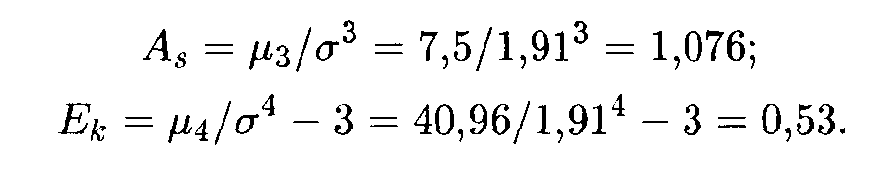
В данном случае «длинная» часть кривой распределения расположена справа от моды, причем сама кривая является несколько более островершинной, чем нормальная кривая с теми же величинами математического ожидания и дисперсии.
Неравенство Чебышева.
Теорема. Для произвольной случайной величины Х и любого числа
Ԑ>0 справедливы неравенства:
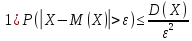
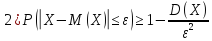
‒ вероятность противоположного неравенства.
Средний расход воды на животноводческой ферме составляет 1000 л в день, а среднее квадратичное отклонение этой случайной величины не превышает 200 л. Оценить вероятность того, что расход воды на ферме в любой выбранный день не превзойдет 2000 л, используя неравенство Чебышева.
Пусть X –расход воды на животноводческой ферме (л).
По условию М(Х) = 1000.
Дисперсия D(X) = . Так как границы интервала 0X 2000 симметричны относительно математического ожиданияМ(Х) = 1000, то для оценки вероятности искомого события можно применить неравенство Чебышева:
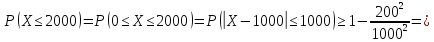
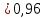

То есть не менее, чем 0,96.
Для биномиального распределения неравенство Чебышева примет вид:
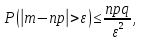
так как M(X) = np; D(X)=npq.
Основные типы распределений НСВ
НСВ Х имеет равномерный закон распределения на отрезке , если её плотность вероятности на этом отрезке постоянна и равна 0 вне его:
Обозначение: XR(a;b).
Проверим условие нормировки:
Функция распределения:
1) ≤ a , тогда .
3) x > b, тогда
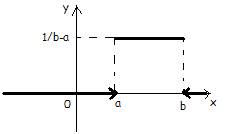
f(x):
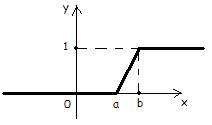
F(x):
Вероятность попадания в интервал (α;β):
Математическое ожидание:
Можно показать (самостоятельно), что
Среднее квадратическое отклонение:
Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчетов, в ряде задач массового обслуживания.
Поезда метрополитена идут регулярно с интервалом 2 минуты. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придётся не больше полминуты? Найти числовые характеристики случайной величины Х — времени ожидания поезда.
2) Показательный закон распределения (экспоненциальный).
НСВ Х имеет показательный закон распределения с параметром λ > 0, если её плотность вероятности:
Обозначение: Х
Проверим условие нормировки:
Функция распределения:
2) x ≥ 0, тогда
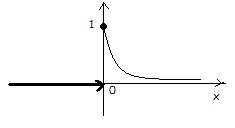
f(x)
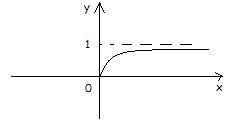
F(x)
Вероятность попадания в интервал (α;β):
Математическое ожидание:
Можно показать (самостоятельно), что
Можно показать, что
Среднее квадратическое отклонение:
Показательный закон распределения играет большую роль в теории массового обслуживания и теории надёжности. Так, например, по показательному закону распределены следующие случайные величины: длительность телефонного разговора, срок безотказной работы прибора, продолжительность жизни атома радиоактивного вещества.
Установлено, что время ремонта телевизоров есть случайная величина, распределённая по показательному закону. Определить вероятность того, что на ремонт телевизора потребуется не менее 20 дней, если среднее время ремонта телевизоров составляет 15 дней. Найти плотность вероятности, функцию распределения, среднее квадратическое отклонение.
=15, следовательно, λ=.
3) Нормальный закон распределения.
НСВ Х имеет нормальный закон распределения с параметрами m, σ, если на всей числовой оси её плотность вероятности:
Обозначение: X
Проверим условие нормировки:
==1, так как, (интеграл Пуассона).
Функция распределения:
Можно показать, что
где — функция Лапласа.
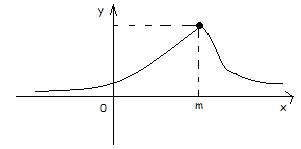
f(x)
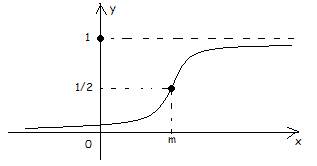
F(x)
Математическое ожидание:
Среднее квадратическое отклонение:
Вероятность попадания в интервал:
Правило «трёх сигм».
Практически достоверное событие, что значения случайной величины, нормально распределенной с параметрами m и заключены в интервале (m-3σ; m+3σ).
Полагая, что рост мужчин определенной возрастной группы есть случайная величина X. Найти , , долю костюмов 4-го роста (176; 182см), которую нужно предусмотреть в общем объеме производства для данной возрастной группы.
Нормальный закон распределения наиболее часто встречается на практике. Главная особенность, выделяющая его среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях. С помощью нормального закона получен ряд важных распределений (логарифмически-нормальное, хи-квадрат, распределение Стьюдента, распределение Фишера-Снедекора).
Познавательно:
Недостатки речного транспорта РЕЧНОЙ ТРАНСПОРТ Речной транспорт (внутренний водный транспорт) — транспорт.
Классификация нормативно-правовых актов Нормативно-правовые акты классифицируются по различным основаниям.
Основные этапы развития астрономии Предмет и задачи астрономии. Разделы астрономии.Классические и современные методы астрономических исследований. Предмет и задачи.
Основные определения и теоремы. Геометрия 8 класс Многоугольник — это фигура, составленная из отрезков так, что смежные отрезки не лежат на одной прямой, а несмежные отрезки не.
Аргументы финансовых функций Excel анализа инвестиций Аргумент Назначение аргумента Даты (дата1, …,датаN) Расписание дат платежей, соответствующее ряду денежных потоков.
Источник https://studme.org/290159/matematika_himiya_fizik/pokazatelnyy_eksponentsialnyy_zakon_raspredeleniya_raspredelenie_veybulla
Источник https://studfile.net/preview/6055012/page:10/
Источник https://studopedia.ru/3_73988_osnovnie-tipi-raspredeleniy-nsv.html





